《数学模型》课程思政优秀教学案例

让数据说话，让模型决策

数学与信息科学学院 花强

课程名称：数学模型

课程性质：专业选修

授课对象：数学类

教学方式：课堂讲授

一、课程简介

数学模型是在合理的简化和假设下，使用数学概念和数学结构来对一个现实对象进行的定量化解释。建立、求解、分析、检验数学模型的过程统称为数学建模。《数学模型》课程以物理、计算机、生命科学、经济、管理等领域的一些典型实例为背景，阐述如何通过建立数学模型和利用相关数学软件（Matlab、Lingo、SPSS）来研究、解决实际问题的基本方法和技能。开设本课程的目的是，通过典型数学模型分析和课外建模实践，使学生基本掌握运用数学知识建立数学模型来研究科研问题或实际课题的基本技能与基本技巧，本课程教学除传授知识外还要求学生在实际建模中注意培养和提高自身的能力，以提高自己的综合素质与实际本领。通过典型建模实例的分析和参加建模实践活动，培养和增强学生自学能力、创新素质。本课程包括一定学时的讨论班，学生可利用课外时间自己参与建模实践活动并自愿参加由指导教师组织的讨论班活动。选修本课程的本科生经双向选择还有机会参加全国大学生数学建模竞赛和美国大学生数学建模竞赛。注重提高学生的创新精神和实践能力，培养应用型、复合型的优秀人才。

二、“课程思政”总体设计情况

立德树人是教育的根本任务，做好数学“课程思政”，深度挖掘“思政元素”是实现这一任务的根本保障。数学模型课程基于学校和专业人才培养要求对“课程思政”进行了认真的设计和实践，达到数学建模课程与思想政治理论课同向同行，形成协同效应的目标。

一方面将思想水平、价值理想等思政元素纳入课程标准，落实立德树人根本任务，体现为党培养社会主义建设者与接班人的目标。同时，注重加强数学素质教育和实践应用能力提升，体现为国培养复合型高素质人才目标；

另一方面，课程内容进行调整，紧跟时代步伐，增添围绕“抗击疫情”、“航天探月”、“乡村振兴”等主题，调整授课内容，在教授数学建模技能和知识的同时，自然融合了社会担当及家国情怀，民族自信和科技自信，实时开展了课程思政育人实践。本课程德育与思政教育融入点清单如下表。

表1课程德育与思政教育融入点

三、“课程思政”教学实施思路

根据数学专业学生特点和模型课程特点，提升思政元素融入课堂需要教学团队教师改进和灵活运用教学方法，积极探索并创新课程思政建设的模式和路径。基本实施思路如下：

1. 增强数学模型课程立德育人功能

数学模型课程要突出培育科学精神、探索创新精神，注重把辩证唯物主义、历史唯物主义贯穿渗透到课程教学中，注重把爱国主义、民族情怀贯穿渗透到课程教学中，引导学生增强人与自然和谐共生意识，明确人类共同发展进步的历史担当。

1. 加强数学模型课程思想价值引领

数学模型课程的教学过程中，重点培养学生实事求是、崇尚科学、实践创新、精益求精的精神，同时培养学生严谨认真、勇于探索、逐本溯源、追求卓越的优秀品质，使得学生成长为心系社会并有担当的技术性人才。将价值导向与知识传授相融合，在知识传授和能力培养中，弘扬社会主义核心价值观，传播爱党、爱国的积极向上的正能量，将思想价值引领贯穿教学所有环节。

1. 提炼数学模型课程德育元素特色

数学模型是建立在数学世界与现实世界的一座桥梁，她让同学们在理性与感性、定量与定性、演绎与归纳、分析与综合中充分认识世界，继而增强发现世界、改造世界的能力。课程的特点是从数学方法出发案例式讲授分析模型建立与解释等。在案例中融入思政元素并不是重点，而从中提炼课程德育元素的特色，是我们教学团队更值得研究和追求的事情。因此教学团队着重围绕“备内容、备学生、备教法”，发挥团队合力，凝聚智慧，提升课程思政教学特色和效果，不断总结经验，优化教法，深化落实“三全育人”教育理念。

四、教学特色与创新

做好数学“课程思政”，深度挖掘“思政元素”是把立德树人作为教育的根本任务这一理念的重要体现。我们提炼出的在数学模型课程中的思政特色包括以下四个方面：

（一） 勤“滴灌”，严谨科学态度

采用“滴灌方式”将“思政”元素渗透各教学环节，借助猜测、验证、归纳、演绎的建模典型手段，培养学生科学精神，用严谨的态度去面对和解决现实复杂世界的问题，初步具备正确的学习探究思维和方法，为建立正确的世界观、人生观、价值观打下坚实基础。从表1中可以看到，用数学讲好思政元素，有理有据，深入人心。

（二） 重能力，崇尚理性思维

数学建模是培养理性思维的重要工具和途径。对理性思维的崇尚则随着学生数学建模能力的提高而树立起来，也必将能够体会到理性思维给自身成长带来的收获。让学生具备了正确的学习理念、学习方法和正确的认知、发展和创新。

（三） 追本源，阐释人生哲学

数学与哲学的天然关联，使得在数学建模丰富的案例讲解中，能够直接帮助学生见微知著，格物致知。从事物的本质和原理中自然获得人生哲学。我们可以顺利地把“课程思政”工作贯穿教学全过程，实现知识传授、能力培养与价值引领的有机统一。

（四） 树正气，涵养家国情怀

通过引入数学故事、举行数模竞赛、典型建模案例分析方式，让学生在学习数学建模课程同时，增强民族自豪感，形成正确理想信念和为祖国建设服务，为人民服务的意识和觉悟，养正家国情怀。

下面我就用一次课堂案例《建模教师眼中的COVID-19》来具体阐述思政与课程的融合。

1. 课程题目：

   疫情预测模型——建模教师眼中的COVID-19

1. 课程课时：2学时

2. 课程内容

在合理的基本假设下，借助微积分工具，引导学生逐步构建模拟传染病传播的SIR模型。根据SIR模型的特点，利用前置章节所学知识给出关键参数讨论：日接触率λ，日治愈率μ，这个过程可以培养学生抓住本质，遵循数理逻辑、进行科学探究能力。

结合历史及当下COVID-19的传播，查阅传播数据，培养学生综合应用信息技术的能力，利用Matlab软件对历史数据来进行预测分析，培养学生综合应用相关的信息技术从科学的观点认知世界的能力。

1. 思政内容与育人目标

1.马克思辩证唯物主义，培养学生科学的世界观。

在SIR模型的建立、推导以及求解过程中，引导学生正确认识传染病发展的本质规律，从辩证的角度看待事物，科学的认知防疫和抗疫政策，对比东西方抗疫差异和产生原因。

2.增强民族自信和爱国主义。

在教学过程中，通过COVID-19疫情的中外显著差别，坚定学生对党的领导，社会主义制度的认同，拥护国家的防疫政策，理解学校采取的相关决定，培养学生对数学的兴趣和专业的自信，增强学生民族自豪感和爱国主义情怀。

3.新时代青年的责任和使命担当。

通过微分方程的科学解释，使学生理解COVID-19疫情传播的决定因素，使学生能够清楚认知当代青年在国家面临重大事件时该有的责任和担当，帮助学生树立勇攀科学高峰，为中华民族伟大复兴的信心和目标。

1. 案例设计与教学过程

1.引入

通过展示新冠肺炎疫情在中国、美国等国家的传播，并列明防疫成果的显著差异，使学生非常直观的树立民族自豪感，初步坚定社会主义制度自信，提出问题并引出今天的主题：传染病模型。

2.传染病模型的建立

通过微积分基本理论和基于对传染病发病到结束过程的基本假设建立传染病的微分方程模型。

主要假设包含：

假设人口总数不变，人群划分为三部分：S(t)是t时刻易感人群比例；I(t)是t时刻感染人群比例；R(t)称为移出者比例。此时S(t)+I(t)+R(t)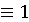

易感人群与感染人员接触时被传染，传染率为λ，在单位时间内被所有病人传染的人数比例为λSIN。

单位时间内从染病者中移出的人数与病人数量成正比，比例系数为μ，单位时间内移出者的比例为μI。

基于以上四条假设，可建立如下微分方程组(SIR模型)：

3.传染期接触数

通过对方程组(1)的观察，可以直接分析前两个方程。

首先，将方程组中的前两个方程作比值，得到：

对方程(2)采用变量分离法求解得到：

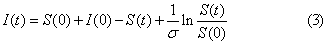
其中，σ=λ/μ，假设初始时刻无感染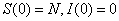：，我们可知感染人数可能达到的最大值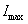是：

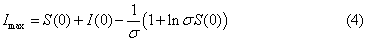
可以看到最大感染比例是传染期接触数的增函数，即大的传染期接触数导致更为严重的疫情。而传染期接触数与传染病的传染能力，对传染病的控制能力直接相关。基本结论就是：提高当地卫生水平和增强当地医疗水平，都能大大提高传染病的防控能力。

4. 新冠肺炎疫情传播分析

通过建立的SIR模型以及上一部分给出的基本再生数来分析COVID-19在中美印三国的传播实况。利用相关的数值计算软件，基于疫情的实时数据驱动估计关键参数，进一步给出三国新冠疫情发展状况。从科学的角度阐述政府和人民群众应该如何应对疫情，让同学们认识到中国共产党的领导是多么正确！国家采取的抗疫和防疫政策是多么的英明！反观分析世界第一大经济体—美国和同为世界人口大国的印度缘何在此方面失败。

1. 教学效果与教学反思

课程思政过程很好的贯彻了“春风化雨入心田，润物无声孕新知”的理念，不是单独把思政模块独立于教学过程中其他模块来进行，摆脱了课程思政与课程内容的泾渭分明，充分做到深度融合和完美切换。通过学生上课状态，学校督导评价，学生评价等多方面表明，教学效果优秀，思政目标达标。 这一案例的实践，使学生脱离说教式思政，潜移默化中培养学生的正确世界观、人生观和价值观。在掌握知识技能的同时，树立为中华民族伟大复兴贡献力量。在爱国情怀核心教育的驱动下，帮助学生树立正确的人生目标，立志为国家、为民族的伟大复兴，寻找到切合实际而又能迎合国家重大战略需求的奋斗目标！

综上所述，我觉得这次的思政案例设计基本是成功的，教学理念和思政设计得到了较好的贯彻，教学过程连贯，教学效果良好。对整体课程的把控，需要在以后的教学中进行更加精准。