一、课程基本信息

1.课程类型：专业选修课

2.课程性质：近世代数不仅在数学中占有及其重要的地位，而且在其他学科中也有广泛的应用，如：理论物理、计算机学科、编码学、密码学等。其研究的方法和观点对其他学科产生了越来越大的影响。为了适应数学本身和社会进步的需要，近世代数的内容需要更新与完善，本课程授课要求保留了原教材的精华，也增加了与计算机学科和思想政治教育相关的内容。本课程性质为专业方向选修课。

3.面向专业：数学与应用数学，金融数学

4.学时：51

5.学分：3

二、课程团队

1.课程负责人简介

课程负责人毛华，女，教授，博士生导师。2002年博士毕业于西安电子科技大学应用数学系，并获博士学位；之后，进入郑州大学数学系博士后流动站，进行博士后研究工作，2005年出站；随后，被引进到河北大学工作至今。自2005年以来连续讲授《近世代数》课程。2012年编著出版教材《近世代数基础》（科学出版社），2018年与杨兰珍合作出版教材《近世代数基础》（第二版，科学出版社），并成为河北大学精品教材， 2019年第二次印刷。该教材可作为数学类和管理类专业相关研究方向的高年级本科生和研究生教材或教学参考书。负责人以“代数论”为基础，近年来（2016年至今）主持河北省自然科学基金面上项目1项（正在办理结项手续）、国家自然科学基金面上项目1项（已结项），发表学术论文50余篇，获批发明专利1项、软件著作权7项。发表课程思政教改论文2篇，获全国高校教师网络培训中心思政专题研修学习班证书。负责人主持的“近世代数”入选河北大学第二批“课程思政改革试点课程”建设项目。负责人主讲的《近世代数》课程被评为河北大学2020年“课程思政”优秀课程。

2.课程团队主要成员简介（附团队成员合影1张）

课程团队主要成员杨兰珍，女，副教授。近年来，承担《近世代数》课程教学。之外，还承担“大学数学C(概率统计I)、大学数学C(概率统计II)、大学数学B(概率论与数理统计)、模糊数学基础、大学数学C(线性代数II)、大学数学C(线性代数I)、线性代数、图论等课程”等课程教学，并且指导本科毕业论文多人。2018年与毛华教授合作，编著教材《近世代数基础》(第二版)。此外，还参与研究生教学，并于2016年赴美国佐治亚州立大学研修，提升自己的专业知识。授课中注重将课程思政融入课程教学，育人目标主要为：1.树立正确的世界观、人生观、价值观；2.培养学生创新意识、工匠精神、自主学习能力与团队协作精神；3.爱国、守法，养成良好的行为习惯，弘扬社会主义核心价值观。近期获得如下荣誉：1.获得2010-2011学年教学质量优秀、2013-2014学年教学质量优秀、2017-2018学年教学质量优秀；2.获2010年度年终考核优秀、2017年度年终考核优秀；3.2013年，获河北省教学成果奖一等奖（排名第5）。

三、课程思政教学理念与目标

根据《近世代数》数学理论的组成可知，数学教学过程是由数学概念、命题和小结等元素组成。数学命题是由数学概念组合而成，反映了数学概念之间的关系，所以在学习的复杂度方面高于概念的学习。再根据《近世代数》教学教育规律可知，数学命题是《近世代数》课堂教学的主要内容，结合《近世代数》数学命题自身数学特性，在命题的引进和应用，以及教学课程的小结中可以结合党史和新中国史，寻找到合适的思政教育内容。将思想教育内容以命题知识的引进、应用、例题和实例的方式呈现，将思想元素以提纲絜领方式表现在小结中，以这种既能完成数学知识的传授，又能将党的思想政治教育内涵进行传播。使得在数学课堂教学中，用润物无声的方式，完成提升学生热爱党、热爱国家的情怀，实现数学和思政两个教育同步进行。落实习近平同志提出的“把思想政治工作贯穿教育教学全过程”的思想，在数学课堂教学中的实现。

这种教学过程改变了以往仅仅是数学知识传授的课堂教学，而是在传授“近世代数”知识的同时，进行思想政治教育，加强了学生爱党爱国的情怀。达到了教学改革之目的，即落实我党的教育方针，立德树人。

四、课程思政教学设计

1.课程思政教学内容。根据高校数学课程的课堂教学规律，结合中国共产党党史，将自然科学理论与中国革命实际有机结合，主要包括以下三部分的研究内容，完成“近世代数”思政资源挖掘的探索教学内容。

第一部分，研究中国共产党发展历史以及我党在中国革命的每个阶段中，对当时革命发展所起的促进作用；研究新中国事业发展中，我党的路线方针和政策，以及党的引领作用；研究习近平新时代中国特色社会主义思想指导下，党和国家在各方面工作中所取得的成就；研究习近平高等教育思想和指示精神。

第二部分，研究《近世代数》数学课程在一堂课中，所要进行讲授的数学命题数学内容自身所含知识；研究相关的命题等产生的原因；研究这些命题等数学知识在科学发展中的应用；研究所授课程班级学生的专业特点，以及学生把握数学知识的能力和程度；研究学生对党的知识和爱国知识的掌握情况。

第三部分，研究如何根据上述内容，找到对于课堂要进行授课的数学内容，与第一部分研究内容可以结合的部分；研究如何将结合的内容在课堂上完成讲授。

2. 教学方法与举措。以往的授课方式仅仅是讲授数学知识，而在课程思政教学设计中，将所要讲授的《近世代数》课程内容用命题或小结等数学内容基础，融合我党的历史和新中国史中的一些内容，反复酝酿，多次尝试，建立合适于此命题或此小结等的数学模型，用此模型引入所讲命题或小结等，再用此模型说明所讲授的命题或小结等的应用，从而完成在一个命题或其他数学内容传授中，对学生进行党史和新中国史的思想教育工作。

3.《近世代数》课程思政—教学设计的一个具体实例表现

以河北大学数学与应用数学专业和金融数学专业开设的《近世代数》课程课本的第一章小结为例，说明挖掘数学课程一章小结中思政资源的探寻过程。

第一章主要讲述了泛代数最基本的研究内容、组织结构。经典代数是一个集合的特征函数取值为0和1两个值的代数，函数取值为0和1的原像必为二个互不相交的集合，简称为二支，对不同的分支采取不同的研究方案，在逻辑学中属于二支决策。在此思维下，一是研究一个代数的“子”和“商”问题；二是研究“直积”问题；三是研究两个代数之间的关系问题。另外，若将一个集合的特征函数取值扩充为0、1和区间(0,1)上，在模糊数学中称此函数为隶属函数，则构成模糊代数的研究。函数取值为0、1和区间(0,1)的原像为三个互不相交的集合，简称为三支，对三支采取不同的研究对策，在逻辑学中属于三支决策。模糊代数也有类似经典代数的研究内容（分析过程见图.1）

图.1

党史相关知识是：1940年，经过认真地分析当时中国各方政治势力的具体情况，为了达到抗日战争胜利目的，毛泽东同志提出必须采取发展进步势力、争取中间势力、反对顽固势力的抗日战争统一战线。

将上述党史知识与第一章小结内容结合如下：若设中国各方政治势力为一个集合A，取值1(0)为坚决(阻碍)抗日的势力，取值(0,1)为抗日的中间派势力，则确定了A上的一个模糊集，得到A的一个隶属函数。这是一个模糊代数的模型。在毛泽东同志统一战线思想的指导下，中国人民团结抗日，最终取得了抗日战争的胜利（分析过程见图.2）。

图.2

该案例表明，经典代数与模糊代数之间是不能有替代关系，是相互依存的，它们的产生是由解决不同实际问题导致的。

与此内容相关论文已发表在《教育教学论坛》2020年7月，第30期。

（《教育教学论坛》第30期杂志封皮、文章第一页截图）

五、课程思政教学效果与学生评价

《近世代数》课程团队在2020-2021学年秋学期的学生问卷中评教成绩分别是97.79%和98.17%。

2020-2021年《近世代数》课程学生评教截图1

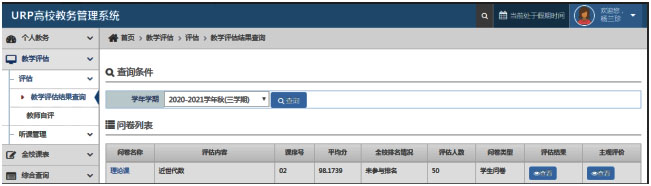
2020-2021年《近世代数》课程学生评教截图2

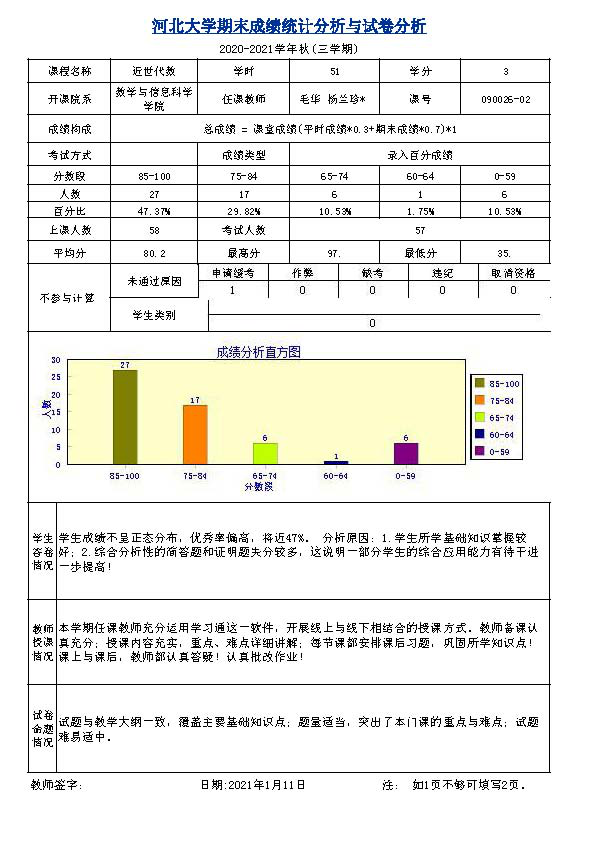
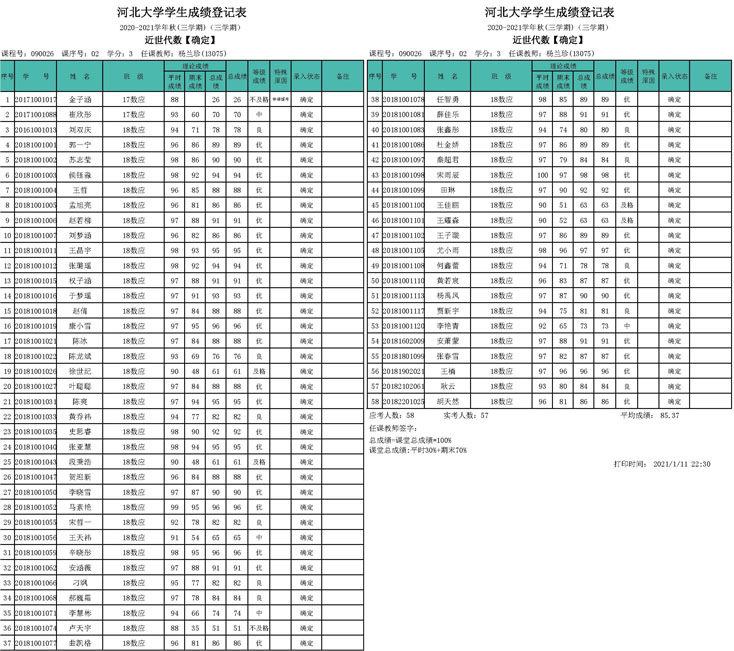
2020-2021年学生成绩登记表截图

五、教学反思                                    

从《近世代数》第一章小结看出，虽然数学课不像思政课那样，可以进行“显性”的思政教育，但是仍然有“隐性”的红色思想。本设计中的第一章小结中思政教育资源的挖掘探查路径，用于其他方式的数学课程小结，以及其他非思政课程中进行相关内容小结，也有借鉴意义。

课堂是学校传播知识的主要载体，在教授专业知识和技能的同时，传播马克思主义思想和社会主义价值观，使得学校成为化育为人的天地。在课程设计时要站在立德树人的战略高度，改变以往只是单一传授数学知识模式，使学生们同时接受党史和新中国史教育，增强学生爱党、爱国的情怀。

七、其他

1.在课堂教学中，可以留给学生们一些思考题，例如《近世代数》某小结内容或命题内容，如何与自己家乡在十八大之后的变化相联系、如何与校园文化相联系等等。

2.由于教学的基本组成是一样的，因此，这里的教学理念和方法对数学以及其他学科的课程教学理念也有可借鉴的意义。